A Copper Calorimeter Can With Mass 0.446 Kg

Chapter 5. Thermochemistry

5.2 Calorimetry

Learning Objectives

By the finish of this department, you will be able to:

• Explicate the technique of calorimetry
• Calculate and interpret heat and related backdrop using typical calorimetry data

One technique nosotros can apply to measure out the amount of heat involved in a chemic or physical process is known as calorimetry. Calorimetry is used to measure out amounts of heat transferred to or from a substance. To practise so, the heat is exchanged with a calibrated object (calorimeter). The modify in temperature of the measuring part of the calorimeter is converted into the amount of rut (since the previous calibration was used to constitute its heat capacity). The measurement of heat transfer using this approach requires the definition of a organisation (the substance or substances undergoing the chemical or physical modify) and its environs (the other components of the measurement apparatus that serve to either provide heat to the organisation or blot estrus from the organization). Noesis of the heat chapters of the surround, and conscientious measurements of the masses of the system and surroundings and their temperatures before and after the process allows one to calculate the heat transferred as described in this department.

A calorimeter is a device used to mensurate the corporeality of heat involved in a chemical or physical process. For example, when an exothermic reaction occurs in solution in a calorimeter, the estrus produced by the reaction is absorbed past the solution, which increases its temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases its temperature (Effigy 1). The temperature change, forth with the specific oestrus and mass of the solution, can then be used to calculate the amount of oestrus involved in either case.

Figure 1. In a calorimetric determination, either (a) an exothermic process occurs and heat, q, is negative, indicating that thermal energy is transferred from the organization to its environment, or (b) an endothermic process occurs and heat, q, is positive, indicating that thermal energy is transferred from the surroundings to the system.

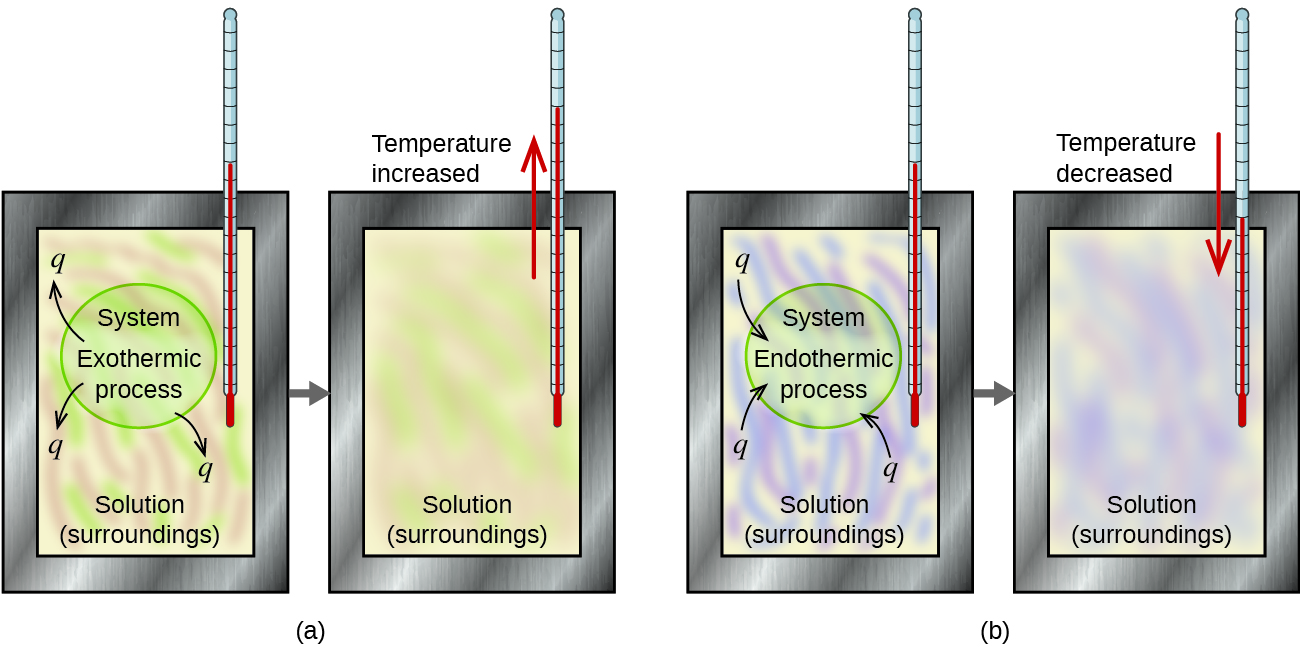
Scientists use well-insulated calorimeters that all but forbid the transfer of heat betwixt the calorimeter and its environment. This enables the authentic determination of the heat involved in chemic processes, the free energy content of foods, and so on. General chemistry students often use simple calorimeters synthetic from polystyrene cups (Figure two). These piece of cake-to-use "coffee cup" calorimeters allow more heat exchange with their environment, and therefore produce less accurate energy values.

Effigy 2. A simple calorimeter tin be synthetic from two polystyrene cups. A thermometer and stirrer extend through the cover into the reaction mixture.

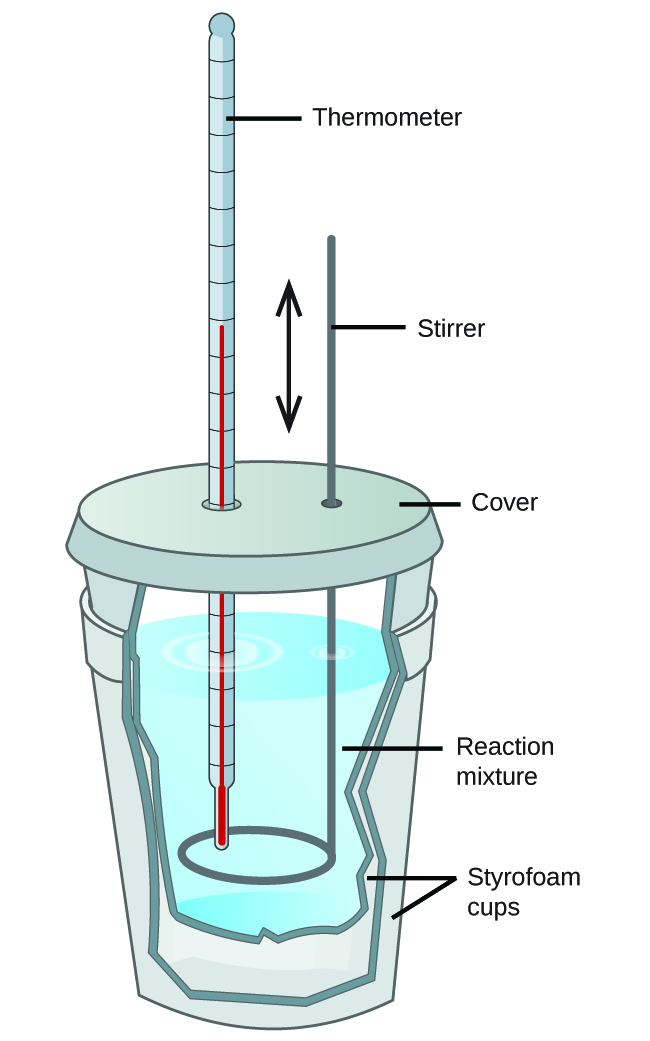
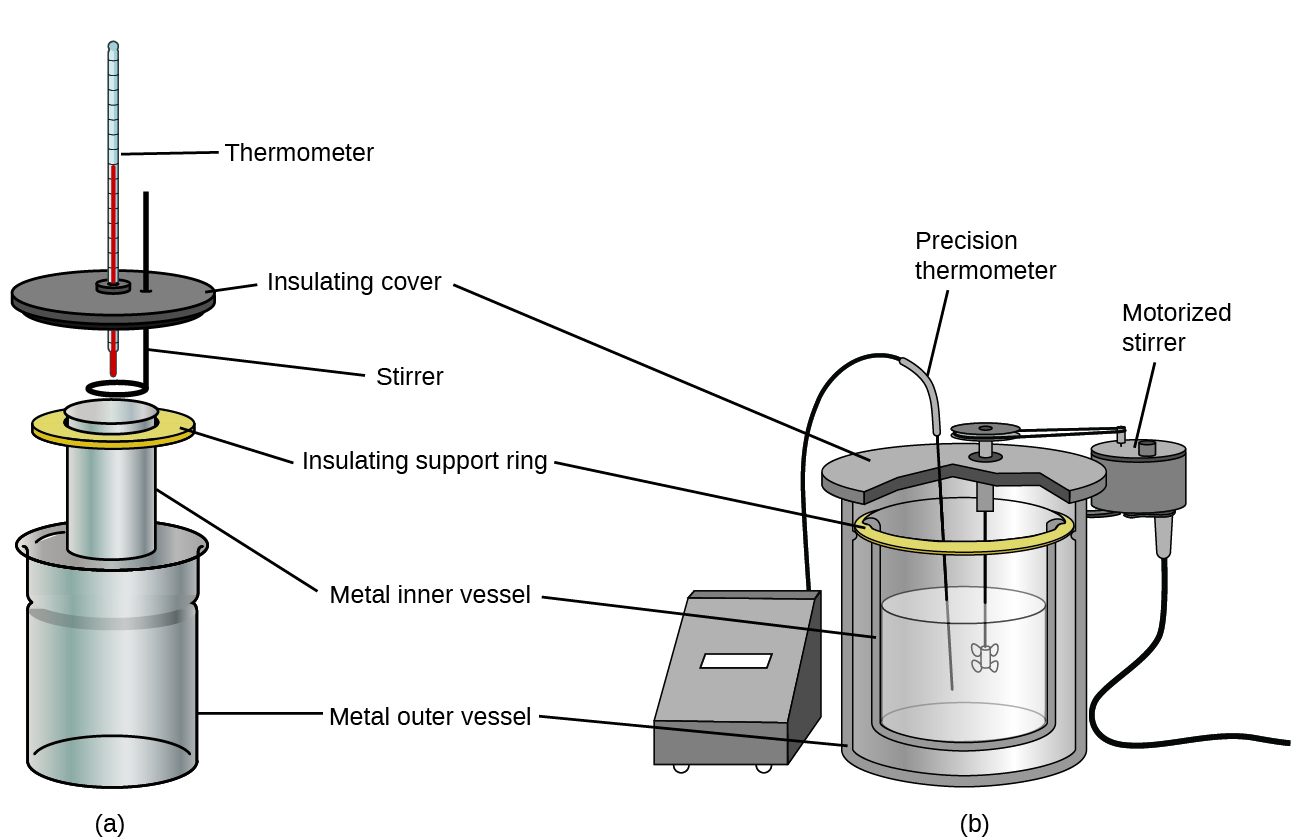
Commercial solution calorimeters are also bachelor. Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal contact during use, along with an insulated cover, handheld stirrer, and simple thermometer. More expensive calorimeters used for industry and research typically take a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more than authentic temperature sensor (Effigy 3).

Figure 3. Commercial solution calorimeters range from (a) simple, inexpensive models for student use to (b) expensive, more authentic models for manufacture and research.

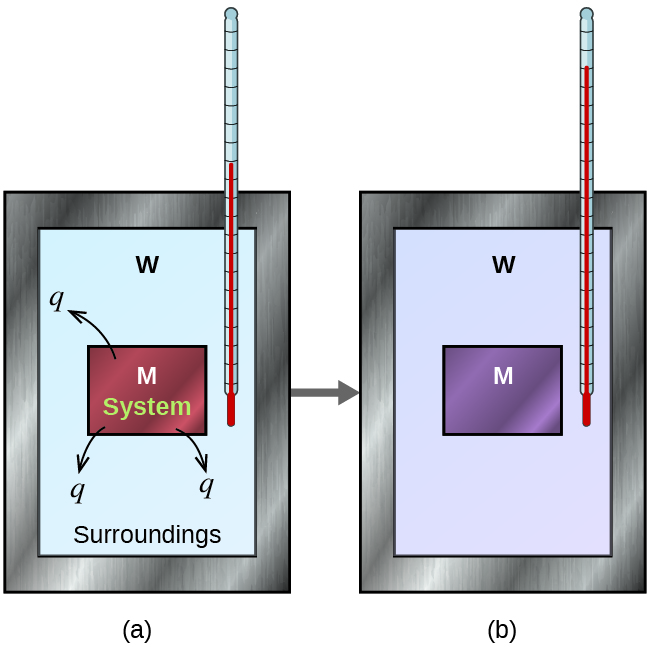
Earlier we practice calorimetry problems involving chemical reactions, consider a simpler example that illustrates the core thought behind calorimetry. Suppose we initially take a high-temperature substance, such as a hot piece of metal (Chiliad), and a depression-temperature substance, such as cool water (W). If we place the metallic in the water, heat will period from Grand to W. The temperature of Grand will decrease, and the temperature of W will increment, until the two substances take the same temperature—that is, when they reach thermal equilibrium (Figure 4). If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no estrus gained or lost by either the calorimeter or the calorimeter'due south environs. Under these platonic circumstances, the internet heat change is zip:

[latex]q_{\text{substance M}} + q_\text{substance W} = 0[/latex]

This relationship can be rearranged to show that the heat gained by substance Grand is equal to the heat lost past substance W:

[latex]q_{\text{substance Chiliad}} = - q_{\text{substance W}}[/latex]

The magnitude of the rut (modify) is therefore the same for both substances, and the negative sign merely shows that q _{substance M} and q _{substance Due west} are opposite in management of heat flow (gain or loss) but does non betoken the arithmetics sign of either q value (that is determined by whether the thing in question gains or loses heat, per definition). In the specific situation described, q _{substance Thou} is a negative value and q _{substance W} is positive, since heat is transferred from M to W.

Figure 4. In a simple calorimetry procedure, (a) heat, q, is transferred from the hot metallic, Thousand, to the cool h2o, W, until (b) both are at the aforementioned temperature.

Instance 1

Heat Transfer between Substances at Different Temperatures
A 360-k piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water was measured every bit 42.seven °C. Calculate the initial temperature of the slice of rebar. Assume the specific heat of steel is approximately the aforementioned as that for atomic number 26 (Table 1 in Chapter 5.1 Energy Nuts), and that all heat transfer occurs between the rebar and the h2o (there is no heat substitution with the surroundings).

Solution
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs estrus. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all oestrus transfer was betwixt the rebar and the h2o, with no heat "lost" to the surroundings, so heat given off by rebar = −estrus taken in past h2o, or:

[latex]q_{\text{rebar}} = -q_{\text{water}}[/latex]

Since we know how rut is related to other measurable quantities, nosotros accept:

[latex](c \times thou \times \Delta T)_{\text{rebar}} = -(c \times m \times \Delta T)_{\text{water}}[/latex]

Letting f = final and i = initial, in expanded class, this becomes:

[latex]c_{\text{rebar}} \times m_{\text{rebar}} \times (T_{\text{f, rebar}} - T_{\text{i, rebar}}) = -c_{\text{water}} \times m_{\text{h2o}} \times (T_{\text{f, water}} - T_{\text{i, water}})[/latex]

The density of water is 1.0 g/mL, then 425 mL of h2o = 425 g. Noting that the final temperature of both the rebar and h2o is 42.7 °C, substituting known values yields:

[latex](0.449 \;\text{J/thousand} \;^\circ\text{C})(360 \;\text{g})(42.7 \;^\circ\text{C} - T_{\text{i, rebar}}) = (4.184 \;\text{J/g} \;^\circ\text{C})(425 \;\text{g})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})[/latex]

[latex]T_{\text{i, rebar}} = \frac{(4.184 \;\text{J/g} \;^\circ\text{C})(425 \;\text{k})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})}{(0.449 \;\text{J/g} \;^\circ\text{C})(360 \;\text{g})} + 42.vii \;^\circ\text{C}[/latex]

Solving this gives T _i,rebar= 248 °C, so the initial temperature of the rebar was 248 °C.

Check Your Learning
A 248-g slice of copper is dropped into 390 mL of water at 22.6 °C. The last temperature of the h2o was measured equally 39.9 °C. Calculate the initial temperature of the slice of copper. Assume that all heat transfer occurs between the copper and the water.

Answer:

The initial temperature of the copper was 335.six °C.

Check Your Learning
A 248-thou piece of copper initially at 314 °C is dropped into 390 mL of water initially at 22.6 °C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature.

Answer:

The last temperature (reached by both copper and h2o) is 38.eight °C.

This method can besides be used to determine other quantities, such every bit the specific oestrus of an unknown metal.

Example 2

Identifying a Metal by Measuring Specific Heat
A 59.7 g slice of metal that had been submerged in boiling water was speedily transferred into 60.0 mL of h2o initially at 22.0 °C. The terminal temperature is 28.5 °C. Utilise these data to determine the specific heat of the metal. Utilize this effect to identify the metal.

Solution
Assuming perfect heat transfer, rut given off by metal = −heat taken in by water, or:

[latex]q_{\text{metal}} = -q_{\text{water}}[/latex]

In expanded form, this is:

[latex]c_{\text{metal}} \times m_{\text{metal}} \times (T_{\text{f, metallic}} - T_{\text{i, metal}}) = -c_{\text{water}} \times m_{\text{water}} \times (T_{\text{f, water}} - T_{\text{i, water}})[/latex]

Noting that since the metal was submerged in boiling h2o, its initial temperature was 100.0 °C; and that for h2o, sixty.0 mL = 60.0 g; we accept:

[latex](c_{\text{metal}}) (59.7 \;\text{thou}) (28.5 \;^\circ\text{C} - 100.0 \;^\circ\text{C}) = -(4.184 \;\text{J/1000} \;^\circ\text{C})(60.0 \;\text{g})(28.5 \;^\circ\text{C} - 22.0 \;^\circ\text{C})[/latex]

Solving this:

[latex]c_{\text{metal}} = \frac{-(4.184 \;\text{J/g} \;^\circ\text{C})(60.0 \;\text{g})(half dozen.five \;^\circ\text{C})}{(59.7 \;\text{1000})(-71.v \;^\circ\text{C})} = 0.38 \;\text{J/g} \;^\circ \text{C}[/latex]

Comparison this with values in Table ane in Chapter five.1 Energy Basics, our experimental specific heat is closest to the value for copper (0.39 J/g °C), so we identify the metal as copper.

Check Your Learning
A 92.9-g piece of a silver/gray metal is heated to 178.0 °C, so quickly transferred into 75.0 mL of h2o initially at 24.0 °C. Subsequently v minutes, both the metal and the water have reached the same temperature: 29.7 °C. Decide the specific heat and the identity of the metal. (Note: You should detect that the specific oestrus is shut to that of 2 dissimilar metals. Explain how you lot can confidently determine the identity of the metal).

Answer:

c _metal= 0.thirteen J/g °C

This specific rut is close to that of either gold or lead. Information technology would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in improver to the value for the specific oestrus indicates that the metal is atomic number 82.

When we use calorimetry to determine the heat involved in a chemic reaction, the same principles we accept been discussing apply. The amount of heat absorbed by the calorimeter is oftentimes modest enough that we can fail information technology (though not for highly accurate measurements, as discussed later), and the calorimeter minimizes energy exchange with the environment. Considering energy is neither created nor destroyed during a chemical reaction, at that place is no overall energy modify during the reaction. The heat produced or consumed in the reaction (the "system"), q _reaction, plus the heat captivated or lost by the solution (the "surroundings"), q _solution, must add together up to zip:

[latex]q_{\text{reaction}} + q_{\text{solution}} = 0[/latex]

This means that the amount of heat produced or consumed in the reaction equals the amount of oestrus absorbed or lost by the solution:

[latex]q_{\text{reaction}} = -q_{\text{solution}}[/latex]

This concept lies at the heart of all calorimetry problems and calculations.

Example iii

Heat Produced by an Exothermic Reaction
When 50.0 mL of 0.10 M HCl(aq) and fifty.0 mL of 0.10 M NaOH(aq), both at 22.0 °C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.nine °C. What is the approximate corporeality of heat produced past this reaction?

[latex]\text{HCl}(aq) + \text{NaOH}(aq) \longrightarrow \text{NaCl}(aq) + \text{H}_2 \text{O}(l)[/latex]

Solution
To visualize what is going on, imagine that you could combine the two solutions so speedily that no reaction took place while they mixed; then subsequently mixing, the reaction took identify. At the instant of mixing, y'all have 100.0 mL of a mixture of HCl and NaOH at 22.0 °C. The HCl and NaOH and then react until the solution temperature reaches 28.ix °C.

The oestrus given off past the reaction is equal to that taken in by the solution. Therefore:

[latex]q_{\text{reaction}} = -q_{\text{solution}}[/latex]

(It is of import to call back that this relationship just holds if the calorimeter does not blot any rut from the reaction, and at that place is no heat exchange between the calorimeter and its environment.)

Adjacent, nosotros know that the oestrus captivated by the solution depends on its specific heat, mass, and temperature modify:

[latex]q_{\text{solution}} = (c \times m \times \Delta T)_{\text{solution}}[/latex]

To go on with this calculation, nosotros demand to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we tin proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × tenⁱⁱ grand (ii significant figures). The specific oestrus of water is approximately 4.18 J/k °C, so we utilize that for the specific heat of the solution. Substituting these values gives:

[latex]q_{\text{solution}} = (4.184 \;\text{J/m} \;^\circ\text{C})(one.0 \times 10^2 \;\text{g})(28.ix \;^\circ\text{C} - 22.0 \;^\circ\text{C}) = 2.89 \times 10^iii \;\text{J}[/latex]

Finally, since we are trying to find the heat of the reaction, nosotros accept:

[latex]q_{\text{reaction}} = -q_{\text{solution}} = -two.89 \times 10^3 \;\text{J}[/latex]

The negative sign indicates that the reaction is exothermic. It produces ii.89 kJ of heat.

Check Your Learning
When 100 mL of 0.200 Chiliad NaCl(aq) and 100 mL of 0.200 M AgNO_three(aq), both at 21.ix °C, are mixed in a coffee cup calorimeter, the temperature increases to 23.5 °C as solid AgCl forms. How much heat is produced by this precipitation reaction? What assumptions did you make to determine your value?

Reply:

1.34 × 10³ J; presume no rut is captivated by the calorimeter, no oestrus is exchanged between the calorimeter and its environment, and that the specific estrus and mass of the solution are the same as those for water

Thermochemistry of Hand Warmers

When working or playing outdoors on a common cold twenty-four hour period, you might use a paw warmer to warm your hands (Figure 5). A mutual reusable hand warmer contains a supersaturated solution of NaC₂H₃O₂ (sodium acetate) and a metal disc. Bending the disk creates nucleation sites around which the metastable NaC₂H_threeO₂ quickly crystallizes (a later chapter on solutions will investigate saturation and supersaturation in more than item).

The process [latex]\text{NaC}_2 \text{H}_3 \text{O}_2 (aq) \longrightarrow \text{NaC}_2 \text{H}_3 \text{O}_2 (south)[/latex] is exothermic, and the heat produced by this process is absorbed past your hands, thereby warming them (at to the lowest degree for a while). If the hand warmer is reheated, the NaC₂H₃O₂ redissolves and tin can be reused.

Figure 5. Chemical hand warmers produce heat that warms your manus on a common cold day. In this one, you can encounter the metal disc that initiates the exothermic precipitation reaction. (credit: modification of work past Science Buddies Television set/YouTube)

Another common mitt warmer produces heat when it is ripped open, exposing iron and water in the manus warmer to oxygen in the air. One simplified version of this exothermic reaction is [latex]two\text{Fe}(southward) + \frac{three}{2}\text{O}_2(g) \longrightarrow \text{Fe}_2\text{O}_3(south)[/latex]. Common salt in the hand warmer catalyzes the reaction, so it produces estrus more rapidly; cellulose, vermiculite, and activated carbon help distribute the heat evenly. Other types of hand warmers apply lighter fluid (a platinum catalyst helps lighter fluid oxidize exothermically), charcoal (charcoal oxidizes in a special case), or electrical units that produce oestrus by passing an electric current from a bombardment through resistive wires.

This link shows the precipitation reaction that occurs when the disk in a chemical hand warmer is flexed.

Example four

Heat Catamenia in an Instant Ice Pack
When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an "instant water ice pack" (Figure 6). When 3.21 1000 of solid NH₄NO₃ dissolves in fifty.0 one thousand of water at 24.ix °C in a calorimeter, the temperature decreases to 20.3 °C.

Calculate the value of q for this reaction and explain the significant of its arithmetic sign. State any assumptions that you lot made.

Figure 6. An instant cold pack consists of a bag containing solid ammonium nitrate and a 2nd bag of h2o. When the pocketbook of water is broken, the pack becomes common cold because the dissolution of ammonium nitrate is an endothermic procedure that removes thermal energy from the h2o. The cold pack then removes thermal energy from your torso.

Solution
We assume that the calorimeter prevents heat transfer between the solution and its external surroundings (including the calorimeter itself), in which case:

[latex]q_{\text{rxn}} = -q_{\text{soln}}[/latex]

with "rxn" and "soln" used every bit shorthand for "reaction" and "solution," respectively.

Assuming also that the specific heat of the solution is the same as that for water, we accept:

[latex]\begin{array}{r @{{}={}} l} q_{\text{rxn}} & -{q_{\text{soln}}} = -(c \times yard \times \Delta T)_{\text{soln}} \\[1em] & -[(4.184 \;\text{J/chiliad} \;^\circ\text{C}) \times (53.2 \;\text{g}) \times (xx.3 \;^\circ\text{C} - 24.nine \;^\circ\text{C})] \\[1em] & -[(4.184 \;\text{J/m} \;^\circ\text{C}) \times (53.ii \;\text{g}) \times (-4.half-dozen \;^\circ\text{C})] \\[1em] & + i.0 \times 10^3 \;\text{J} = +1.0 \;\text{kJ} \stop{array}[/latex]

The positive sign for q indicates that the dissolution is an endothermic process.

Bank check Your Learning
When a three.00-g sample of KCl was added to 3.00 × 10² m of water in a coffee cup calorimeter, the temperature decreased past 1.05 °C. How much heat is involved in the dissolution of the KCl? What assumptions did you make?

Answer:

1.33 kJ; assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself) and that the specific heat of the solution is the same as that for water

If the corporeality of heat absorbed by a calorimeter is too large to fail or if we require more accurate results, then nosotros must take into account the heat absorbed both by the solution and by the calorimeter.

The calorimeters described are designed to operate at abiding (atmospheric) pressure level and are convenient to mensurate heat menstruum accompanying processes that occur in solution. A different type of calorimeter that operates at constant volume, colloquially known as a flop calorimeter, is used to measure the free energy produced by reactions that yield large amounts of heat and gaseous products, such equally combustion reactions. (The term "flop" comes from the observation that these reactions can exist vigorous enough to resemble explosions that would damage other calorimeters.) This blazon of calorimeter consists of a robust steel container (the "bomb") that contains the reactants and is itself submerged in h2o (Figure 7). The sample is placed in the bomb, which is and so filled with oxygen at high pressure. A small electrical spark is used to ignite the sample. The energy produced by the reaction is trapped in the steel flop and the surrounding water. The temperature increase is measured and, along with the known heat capacity of the calorimeter, is used to summate the free energy produced by the reaction. Bomb calorimeters require calibration to determine the oestrus capacity of the calorimeter and ensure accurate results. The calibration is achieved using a reaction with a known q, such equally a measured quantity of benzoic acid ignited by a spark from a nickel fuse wire that is weighed before and after the reaction. The temperature change produced past the known reaction is used to determine the heat capacity of the calorimeter. The calibration is generally performed each time before the calorimeter is used to gather research data.

Figure 7. (a) A bomb calorimeter is used to measure oestrus produced by reactions involving gaseous reactants or products, such as combustion. (b) The reactants are contained in the gas-tight "bomb," which is submerged in h2o and surrounded past insulating materials. (credit a: modification of work by "Harbor1"/Wikimedia commons)

Click on this link to view how a bomb calorimeter is prepared for activity.

This site shows calorimetric calculations using sample data.

Instance five

Flop Calorimetry
When 3.12 1000 of glucose, C_sixH₁₂O_half-dozen, is burned in a bomb calorimeter, the temperature of the calorimeter increases from 23.eight °C to 35.6 °C. The calorimeter contains 775 g of water, and the bomb itself has a heat capacity of 893 J/°C. How much estrus was produced by the combustion of the glucose sample?

Solution
The combustion produces heat that is primarily absorbed past the h2o and the bomb. (The amounts of heat absorbed by the reaction products and the unreacted backlog oxygen are relatively small and dealing with them is across the scope of this text. We will neglect them in our calculations.)

The heat produced past the reaction is captivated past the water and the bomb:

[latex]\begin{array}{r @{{}={}} 50} q_{\text{rxn}} & -({q_{\text{h2o}} + q_{\text{bomb}}}) \\[1em] & -[(4.184 \;\text{J/chiliad} \;^\circ\text{C}) \times (775 \;\text{thou}) \times (35.half-dozen \;^\circ\text{C} - 23.8 \;^\circ\text{C}) + 893\;\text{J/}^\circ\text{C} \times (35.half dozen \;^\circ\text{C} - 23.viii \;^\circ\text{C})] \\[1em] & -(38,300 \;\text{J} + ten,500 \;\text{J}) \\[1em] & -48,800 \;\text{J} = -48.8 \;\text{kJ} \end{assortment}[/latex]

This reaction released 48.7 kJ of heat when 3.12 g of glucose was burned.

Cheque Your Learning
When 0.963 chiliad of benzene, C_sixH₆, is burned in a flop calorimeter, the temperature of the calorimeter increases by viii.39 °C. The bomb has a heat chapters of 784 J/°C and is submerged in 925 mL of water. How much heat was produced by the combustion of the glucose sample?

Since the first one was constructed in 1899, 35 calorimeters accept been congenital to measure the heat produced past a living person.^[1] These whole-body calorimeters of various designs are large enough to hold an individual man. More recently, whole-room calorimeters allow for relatively normal activities to be performed, and these calorimeters generate data that more closely reflect the real globe. These calorimeters are used to mensurate the metabolism of individuals under different environmental conditions, unlike dietary regimes, and with different health conditions, such equally diabetes. In humans, metabolism is typically measured in Calories per mean solar day. A nutritional calorie (Calorie) is the free energy unit used to quantify the amount of energy derived from the metabolism of foods; ane Calorie is equal to 1000 calories (1 kcal), the amount of energy needed to heat 1 kg of water by 1 °C.

Measuring Nutritional Calories

In your day-to-mean solar day life, you may be more familiar with energy being given in Calories, or nutritional calories, which are used to quantify the amount of energy in foods. One calorie (cal) = exactly 4.184 joules, and 1 Calorie (note the capitalization) = g cal, or ane kcal. (This is approximately the amount of energy needed to heat 1 kg of h2o by 1 °C.)

The macronutrients in food are proteins, carbohydrates, and fats or oils. Proteins provide almost 4 Calories per gram, carbohydrates as well provide nigh 4 Calories per gram, and fats and oils provide nearly 9 Calories/k. Nutritional labels on food packages show the caloric content of one serving of the food, also every bit the breakdown into Calories from each of the three macronutrients (Effigy 8).

Figure viii. (a) Macaroni and cheese contain free energy in the form of the macronutrients in the food. (b) The nutrient's nutritional information is shown on the package label. In the US, the energy content is given in Calories (per serving); the remainder of the world usually uses kilojoules. (credit a: modification of work past "Rex Roof"/Flickr)

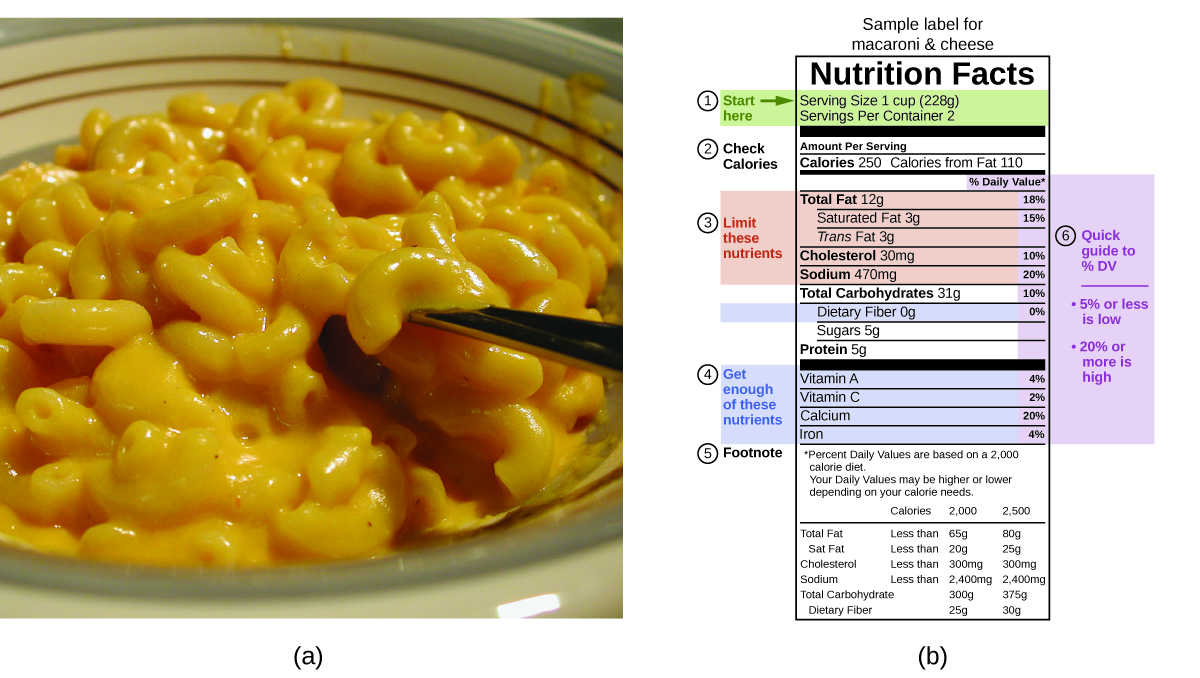
For the case shown in (b), the full energy per 228-g portion is calculated past:

[latex](v \;\text{g protein} \times four \;\text{Calories/yard}) + (31 \;\text{thou carb} \times 4 \;\text{Calories/1000}) + (12 \;\text{g fat} \times 9 \;\text{Calories/g}) = 252 \;\text{Calories}[/latex]

And so, y'all can utilise food labels to count your Calories. Simply where exercise the values come from? And how accurate are they? The caloric content of foods tin exist determined by using bomb calorimetry; that is, by burning the food and measuring the energy it contains. A sample of nutrient is weighed, mixed in a blender, freeze-stale, ground into pulverisation, and formed into a pellet. The pellet is burned within a flop calorimeter, and the measured temperature alter is converted into energy per gram of nutrient.

Today, the caloric content on nutrient labels is derived using a method chosen the Atwater arrangement that uses the boilerplate caloric content of the different chemical constituents of food, protein, sugar, and fats. The average amounts are those given in the equation and are derived from the diverse results given by bomb calorimetry of whole foods. The carbohydrate corporeality is discounted a sure amount for the fiber content, which is boxy carbohydrate. To decide the energy content of a food, the quantities of sugar, protein, and fat are each multiplied by the boilerplate Calories per gram for each and the products summed to obtain the full free energy.

Click on this link to access the Us Department of Agriculture (USDA) National Nutrient Database, containing nutritional information on over 8000 foods.

Key Concepts and Summary

Calorimetry is used to measure the amount of thermal energy transferred in a chemical or concrete process. This requires careful measurement of the temperature change that occurs during the process and the masses of the system and surroundings. These measured quantities are then used to compute the amount of heat produced or consumed in the process using known mathematical relations.

Calorimeters are designed to minimize energy commutation between the system beingness studied and its surroundings. They range from unproblematic coffee cup calorimeters used by introductory chemistry students to sophisticated bomb calorimeters used to determine the energy content of food.

Chemistry Terminate of Chapter Exercises

1. A 500-mL bottle of water at room temperature and a 2-Fifty bottle of water at the same temperature were placed in a refrigerator. After xxx minutes, the 500-mL canteen of h2o had cooled to the temperature of the refrigerator. An hour later, the 2-50 of h2o had cooled to the same temperature. When asked which sample of water lost the most heat, 1 student replied that both bottles lost the aforementioned amount of estrus because they started at the aforementioned temperature and finished at the same temperature. A 2nd student idea that the 2-Fifty canteen of h2o lost more heat because there was more water. A third educatee believed that the 500-mL bottle of water lost more than oestrus because information technology cooled more than apace. A fourth student idea that it was not possible to tell considering we do non know the initial temperature and the final temperature of the water. Signal which of these answers is right and draw the error in each of the other answers.
2. Would the corporeality of rut measured for the reaction in Example iii exist greater, bottom, or remain the same if nosotros used a calorimeter that was a poorer insulator than a coffee cup calorimeter? Explicate your answer.
3. Would the amount of heat absorbed by the dissolution in Case 4 appear greater, lesser, or remain the aforementioned if the experimenter used a calorimeter that was a poorer insulator than a coffee cup calorimeter? Explain your answer.
4. Would the amount of oestrus absorbed by the dissolution in Example iv announced greater, lesser, or remain the same if the estrus capacity of the calorimeter were taken into account? Explain your answer.
5. How many milliliters of h2o at 23 °C with a density of 1.00 yard/mL must be mixed with 180 mL (about 6 oz) of coffee at 95 °C so that the resulting combination will have a temperature of 60 °C? Assume that coffee and water take the same density and the same specific oestrus.
6. How much will the temperature of a cup (180 g) of java at 95 °C be reduced when a 45 g silver spoon (specific heat 0.24 J/g °C) at 25 °C is placed in the java and the two are immune to reach the same temperature? Assume that the java has the same density and specific heat as water.
7. A 45-g aluminum spoon (specific heat 0.88 J/one thousand °C) at 24 °C is placed in 180 mL (180 1000) of coffee at 85 °C and the temperature of the ii become equal.

   (a) What is the concluding temperature when the two become equal? Assume that coffee has the aforementioned specific heat as water.

   (b) The beginning time a student solved this problem she got an respond of 88 °C. Explicate why this is clearly an incorrect answer.

8. The temperature of the cooling water as it leaves the hot engine of an automobile is 240 °F. Afterward it passes through the radiator it has a temperature of 175 °F. Calculate the amount of rut transferred from the engine to the surroundings by one gallon of water with a specific heat of iv.184 J/chiliad °C.
9. A seventy.0-g piece of metal at 80.0 °C is placed in 100 m of water at 22.0 °C contained in a calorimeter like that shown in Figure 2. The metal and water come up to the same temperature at 24.6 °C. How much heat did the metal surrender to the water? What is the specific oestrus of the metal?
10. If a reaction produces one.506 kJ of heat, which is trapped in 30.0 yard of water initially at 26.5 °C in a calorimeter like that in Effigy two, what is the resulting temperature of the h2o?
11. A 0.500-thou sample of KCl is added to 50.0 thou of water in a calorimeter (Figure 2). If the temperature decreases past one.05 °C, what is the approximate amount of heat involved in the dissolution of the KCl, assuming the heat capacity of the resulting solution is 4.18 J/g °C? Is the reaction exothermic or endothermic?
12. Dissolving 3.0 g of CaCl₂(s) in 150.0 g of water in a calorimeter (Effigy 2) at 22.4 °C causes the temperature to rise to 25.8 °C. What is the approximate amount of heat involved in the dissolution, bold the oestrus chapters of the resulting solution is four.18 J/m °C? Is the reaction exothermic or endothermic?
13. When 50.0 k of 0.200 M NaCl(aq) at 24.ane °C is added to 100.0 yard of 0.100 M AgNO₃(aq) at 24.ane °C in a calorimeter, the temperature increases to 25.2 °C equally AgCl(s) forms. Bold the specific estrus of the solution and products is 4.twenty J/g °C, calculate the approximate amount of heat in joules produced.
14. The addition of iii.15 grand of Ba(OH)₂·8H₂O to a solution of 1.52 1000 of NH₄SCN in 100 g of water in a calorimeter acquired the temperature to fall past three.one °C. Bold the specific oestrus of the solution and products is 4.20 J/g °C, calculate the guess amount of heat absorbed by the reaction, which can be represented by the following equation:

    Ba(OH)₂·8H₂O(s) + 2NH₄SCN(aq) ⟶ Ba(SCN)_ii(aq) + 2NH₃(aq) + 10H₂O(l)

15. The reaction of 50 mL of acid and 50 mL of base described in Case 3 increased the temperature of the solution by 6.9 degrees. How much would the temperature have increased if 100 mL of acrid and 100 mL of base of operations had been used in the aforementioned calorimeter starting at the same temperature of 22.0 °C? Explain your respond.
16. If the iii.21 one thousand of NH₄NO₃ in Example iv were dissolved in 100.0 chiliad of water nether the same conditions, how much would the temperature change? Explicate your answer.
17. When one.0 1000 of fructose, C₆H₁₂O_half-dozen(s), a sugar usually found in fruits, is burned in oxygen in a bomb calorimeter, the temperature of the calorimeter increases by 1.58 °C. If the heat capacity of the calorimeter and its contents is 9.90 kJ/°C, what is q for this combustion?
18. When a 0.740-g sample of trinitrotoluene (TNT), C₇H₅Due north_twoO_six, is burned in a bomb calorimeter, the temperature increases from 23.4 °C to 26.ix °C. The rut capacity of the calorimeter is 534 J/°C, and information technology contains 675 mL of water. How much heat was produced by the combustion of the TNT sample?
19. One method of generating electricity is by called-for coal to heat water, which produces steam that drives an electric generator. To make up one's mind the rate at which coal is to be fed into the burner in this type of institute, the rut of combustion per ton of coal must be determined using a bomb calorimeter. When one.00 g of coal is burned in a bomb calorimeter (Figure seven), the temperature increases by ane.48 °C. If the estrus capacity of the calorimeter is 21.6 kJ/°C, determine the heat produced by combustion of a ton of coal (ii.000 × 10³ pounds).
20. The amount of fat recommended for someone with a daily nutrition of 2000 Calories is 65 thou. What percent of the calories in this diet would be supplied by this amount of fat if the boilerplate number of Calories for fat is 9.1 Calories/grand?
21. A teaspoon of the carbohydrate sucrose (common sugar) contains 16 Calories (16 kcal). What is the mass of one teaspoon of sucrose if the average number of Calories for carbohydrates is four.one Calories/grand?
22. What is the maximum mass of carbohydrate in a 6-oz serving of diet soda that contains less than 1 Calorie per can if the average number of Calories for carbohydrates is 4.i Calories/g?
23. A pint of premium water ice foam tin can contain 1100 Calories. What mass of fat, in grams and pounds, must exist produced in the body to store an actress ane.1 × 10³ Calories if the average number of Calories for fat is ix.1 Calories/g?
24. A serving of a breakfast cereal contains 3 g of protein, eighteen yard of carbohydrates, and 6 thousand of fatty. What is the Calorie content of a serving of this cereal if the average number of Calories for fat is 9.one Calories/g, for carbohydrates is 4.ane Calories/one thousand, and for poly peptide is 4.1 Calories/g?
25. Which is the least expensive source of free energy in kilojoules per dollar: a box of breakfast cereal that weighs 32 ounces and costs $4.23, or a liter of isooctane (density, 0.6919 g/mL) that costs $0.45? Compare the nutritional value of the cereal with the oestrus produced by combustion of the isooctane under standard conditions. A 1.0-ounce serving of the cereal provides 130 Calories.

Glossary

bomb calorimeter

device designed to mensurate the free energy modify for processes occurring under conditions of constant volume; unremarkably used for reactions involving solid and gaseous reactants or products

calorimeter

device used to mensurate the amount of heat absorbed or released in a chemical or physical procedure

calorimetry

process of measuring the amount of heat involved in a chemical or physical process

nutritional calorie (Calorie)

unit used for quantifying energy provided by digestion of foods, defined as 1000 cal or ane kcal

surroundings

all matter other than the organization being studied

organization

portion of matter undergoing a chemical or physical modify being studied

Solutions

Answers to Chemistry End of Chapter Exercises

2. lesser; more heat would be lost to the coffee cup and the environment and then ΔT for the h2o would exist lesser and the calculated q would exist lesser

4. greater, since taking the calorimeter'south heat capacity into account will recoup for the thermal energy transferred to the solution from the calorimeter; this arroyo includes the calorimeter itself, along with the solution, as "surroundings": q _rxn = −(q _solution + q _calorimeter); since both q _solution and q _calorimeter are negative, including the latter term (q _rxn) will yield a greater value for the rut of the dissolution

6. The temperature of the coffee will drop 1 degree.

8. 5.7 × 10² kJ

10. 38.v °C

12. two.two kJ; The heat produced shows that the reaction is exothermic.

14. i.iv kJ

sixteen. 22.six. Since the mass and the estrus capacity of the solution is approximately equal to that of the h2o, the two-fold increment in the amount of water leads to a two-fold decrease of the temperature modify.

eighteen. eleven.seven kJ

twenty. 30%

22. 0.24 g

24. 1.four × xⁱⁱ Calories

---

smiththabees02.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/5-2-calorimetry/

Share this post